C Supp. materials for ch. 2

C.1 Bonus structure

We assume that participants represent the distribution of response times conditional on a specific search array as a right-skewed, positive distribution. Here, we assume that internal distributions of response times abide by the rule that

\[\begin{align} log(RT) \sim N(\mu, \sigma) \end{align}\]

where \(\sigma\) is fixed per participant, and \(\mu\) varies as a function of search difficulty.

The participants produces an estimate \(x\). The expected bonus given for a trial is now:

\[\begin{align} E[bonus|x]=Pr_{n \sim N(\mu, \sigma)}[\log(x)>n] \cdot e^{-\log(x)/2}. \end{align}\]

We can write \(log(x)=\mu+\alpha \cdot \sigma\) for some number \(\alpha\). This number represents the position of the estimate relative to the distribution of response times, with lower values corresponding to more risky estimates, and higher values to more conservative ones. Then the expected bonus is:

\[\begin{align} E[bonus|\alpha]&=Pr_{n \sim N(0, 1)}[\alpha>n] \cdot e^{-(\mu+\alpha \cdot \sigma)/2} \\ \nonumber &= Pr_{n \sim N(0, 1)}[\alpha>n] \cdot e^{-(\alpha \cdot \sigma)/2} \cdot e^{-\mu/2}. \end{align}\]

\(\mu\) only appears in the third term in the product, which functions as a constant multiplier which scales the expected bonus equally for all choices of \(\alpha\). It then follows that the function relating the choice of \(\alpha\) to the expected bonus preserves its shape for all possible values of \(\mu\):

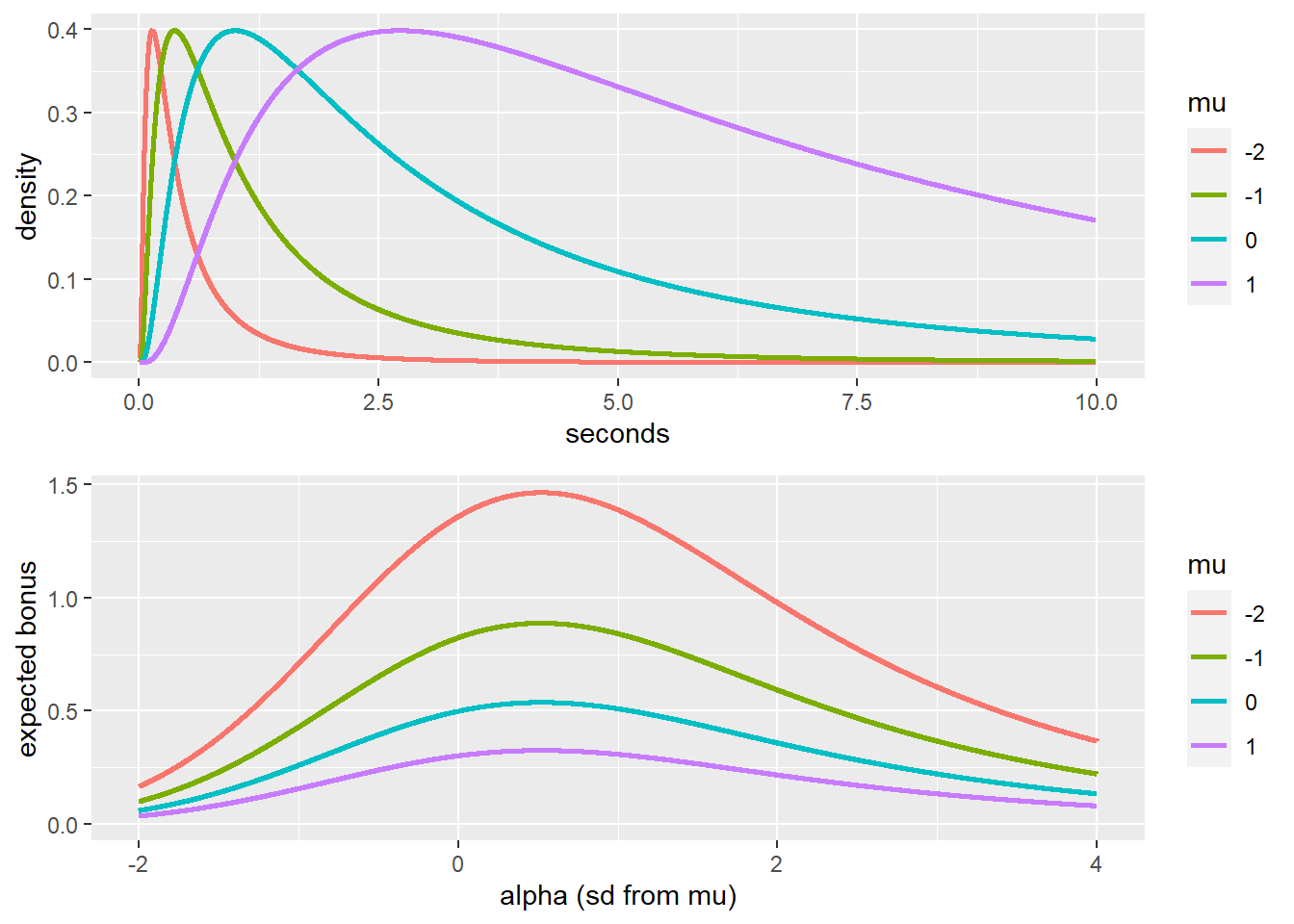
Figure C.1: Upper panel: response time distributions are modeled as exponents of values drawn from a normal distribution with different values of mu. Lower panel: the estimate value that maximizes the expected bonus is fixed with respect to the the mean of the log(RT) distributions, regardless of what the mean is. The expected bonus is higher for lower values of mu, but to maximize their bonus participants should always choose an estimate that is positioned in the 70 quantile of the RT distribution.