Chapter 1 Efficient search termination without task experience: the role of second-order knowledge about visual search

Matan Mazor & Stephen M. Fleming

As a general rule, if it is easy to detect a target in a visual scene, it is also easy to detect its absence. To account for this, models of visual search explain search termination as resulting either from counterfactual reasoning over second-order representations of search efficiency, automatic extraction of ensemble statistics of a display, or heuristic adjustment of a search termination strategy based on previous trials. Traditional few-subjects/many-trials lab-based experiments render it impossible to disentangle the unique contribution of these different processes to absence pop-out - the immediate recognition that a feature is missing from a display. In two pre-registered large-scale online experiments (N1=1187, N2=887) we show that search termination times are already aligned with target identification times in the very first trials of the experiment, before any experience with target presence. Exploratory analysis reveals that second-order knowledge about search efficiency can be used to guide decisions about search termination even if it is not available for explicit report. We conclude that for basic stimulus properties, efficient inference about absence is independent of task experience, and relies instead on implicit second-order knowledge.

1.1 Introduction

Searching for the only blue letter in an array of yellow letters is easy, but searching for the only blue X in an array of yellow Xs and blue Ts is much harder (A. M. Treisman & Gelade, 1980). This difference manifests in the time taken to find the target letter, but also in the time taken to conclude that the target letter is missing. In other words, easier searches not only make it easier to detect the presence of a target, but also to infer its absence. Differences in the speed of detecting the presence of a target have been attributed to pre-attentional mechanisms (A. M. Treisman & Gelade, 1980) and guiding signals (J. M. Wolfe, 2021; J. M. Wolfe & Gray, 2007) that can sometimes make the target item ‘pop out’ immediately without any attentional effort. In target-absent trials, however, there is nothing in the display to pop out. This raises a fundamental question: what makes some decisions about target absence easier than others?

Models of search termination offer three classes of answers to this question, based on counterfactual reasoning, ensemble perception, and task heuristics. According to counterfactual models, decisions about target absence are guided by prior beliefs about search efficiency (“If it were present, I would have found the red book by now”). These comprise beliefs about regularities in the environment (“it it were present, the book would have been on this shelf”), and second-order beliefs about one’s own perception and attention (“the red cover would have immediately drawn my attention”). In recent versions of the Guided Search model (J. M. Wolfe, 2012, 2021), for example, search termination is triggered by a noisy quitting signal accumulator reaching a quitting threshold, which can be adapted to maximize long-time search efficiency, and be affected by prior second-order beliefs about the effects of set size and crowding on search difficulty (J. M. Wolfe, 2012). Similarly, in Competitive Guided Search, the probability of terminating a search is a function of several factors, including a free parameter that indexes counterfactual beliefs about finding a target, had it been present (Moran, Zehetleitner, Müller, & Usher, 2013). Finally, in a fixation-based model of visual search, the number of items that are concurrently scanned within a single fixation (the functional visual field) depends on the expected difficulty of finding a hypothetical target: with more items for easy searches and fewer items for more difficult ones (Hulleman & Olivers, 2017).

Ensemble perception accounts of visual search postulate that some global properties of a display can be extracted automatically and immediately, and that in some cases these global properties are sufficient to conclude that a target is absent. For example, according to Feature Integration Theory, pre-attentive activation in feature maps can provide participants with information about the presence or absence of a feature in the display (A. M. Treisman & Gelade, 1980). The absence of a relevant feature is then sufficient to make an immediate ‘target absent’ decision, without processing any individual stimulus.

Finally, heuristic-based models suggest that quitting parameters are acquired by participants as they perform a task, sometimes by following very simple rules. For example, in one model, an internal activation threshold decreases following incorrect and increases following correct ‘no’ responses (Chun & Wolfe, 1996). A higher activation threshold results in the scanning of less distractors, giving rise to shorter search times for easier searches. This simple heuristic provides an excellent fit to data from a visual search task with hundreds of trials, and does so without requiring that subjects hold any prior knowledge or expectations about search efficiency.

In traditional visual search experiments, where participants perform hundreds of trials of similar searches, it is impossible to disentangle the contributions of these three putative mechanisms to search termination. Yet, the three accounts make different predictions for the earliest trials of a visual search experiment, where participants encounter the stimuli for the first time. In these trials, quitting time cannot reflect the adaptive adjustment of a threshold based on previous trials, or the statistical learning of regularities in the experiment. Instead, efficient search termination without task experience must rely on an immediate perception of ensemble properties of the display, prior second-order knowledge about one’s own search efficiency, or a combination of both.

In two pre-registered experiments we focus on feature search for colour and shape. Focusing on the first four trials of the task, we ask whether prior experience with the task and stimuli is necessary for efficient search termination in feature searches. Unlike typical visual search experiments that comprise hundreds or thousands of trials, here we collect only a handful of trials from a large pool of online participants. This unusual design allows us to reliably identify search time patterns in the first trials of the experiment. By making sure that the first displays do not include the target stimulus, we are able to ask what knowledge is available to participants about their expected search efficiency prior to engaging with the task.

To anticipate our results, we find that efficient search termination for single features does not depend on task experience. In an exploratory analysis on a subset of participants, we further show that efficient search termination is also independent of explicit metacognitive knowledge about the task. We argue that without second-order knowledge about one’s own perception and attention, ensemble perception alone is not sufficient for efficient search termination, and interpret our results as revealing a role for implicit second-order knowledge of search efficiency in search termination.

1.2 Experiment 1

In Experiment 1, we examined search termination in the case of colour search. When searching for a deviant colour, the number of distractors has virtually no effect on search time (colour pop-out; e.g., D’Zmura, 1991), for both ‘target present’ and ‘target absent’ responses. Here we asked whether efficient quitting in colour search (color absence pop-out) is dependent on task experience. A detailed pre-registration document for Experiment 1 can be accessed at osf.io/yh82v/.

1.2.1 Participants

The research complied with all relevant ethical regulations, and was approved by the Research Ethics Committee of University College London (study ID number 1260/003). 1187 Participants (median reported age: 33; range: [18-81]) were recruited via Prolific, and gave their informed consent prior to their participation. They were selected based on their acceptance rate (>95%) and for being native English speakers. Following our pre-registration, we collected data until we reached 320 included participants for each of our pre-registered hypotheses (after applying our pre-registered exclusion criteria). The entire experiment took around 3 minutes to complete (median completion time: 3.19 minutes). Participants were paid £0.38 for their participation, equivalent to an hourly wage of £ 7.14.

1.2.2 Procedure

A static version of Experiment 1 can be accessed on matanmazor.github.io/termination. Participants were first instructed about the visual search task. Specifically, that their task is to report, as accurately and quickly as possible, whether a target stimulus was present (press ‘J’) or absent (press ‘F’). Then, practice trials were delivered, in which the target stimulus was a rotated T, and distractors rotated Ls. The purpose of the practice trials was to familiarize participants with the structure of the task. For these practice trials the number of items was always 3. Practice trials were delivered in short blocks of 6 trials each, and the main part of the experiment started only once participants responded correctly on at least five trials in a block (see Figure 1.1).

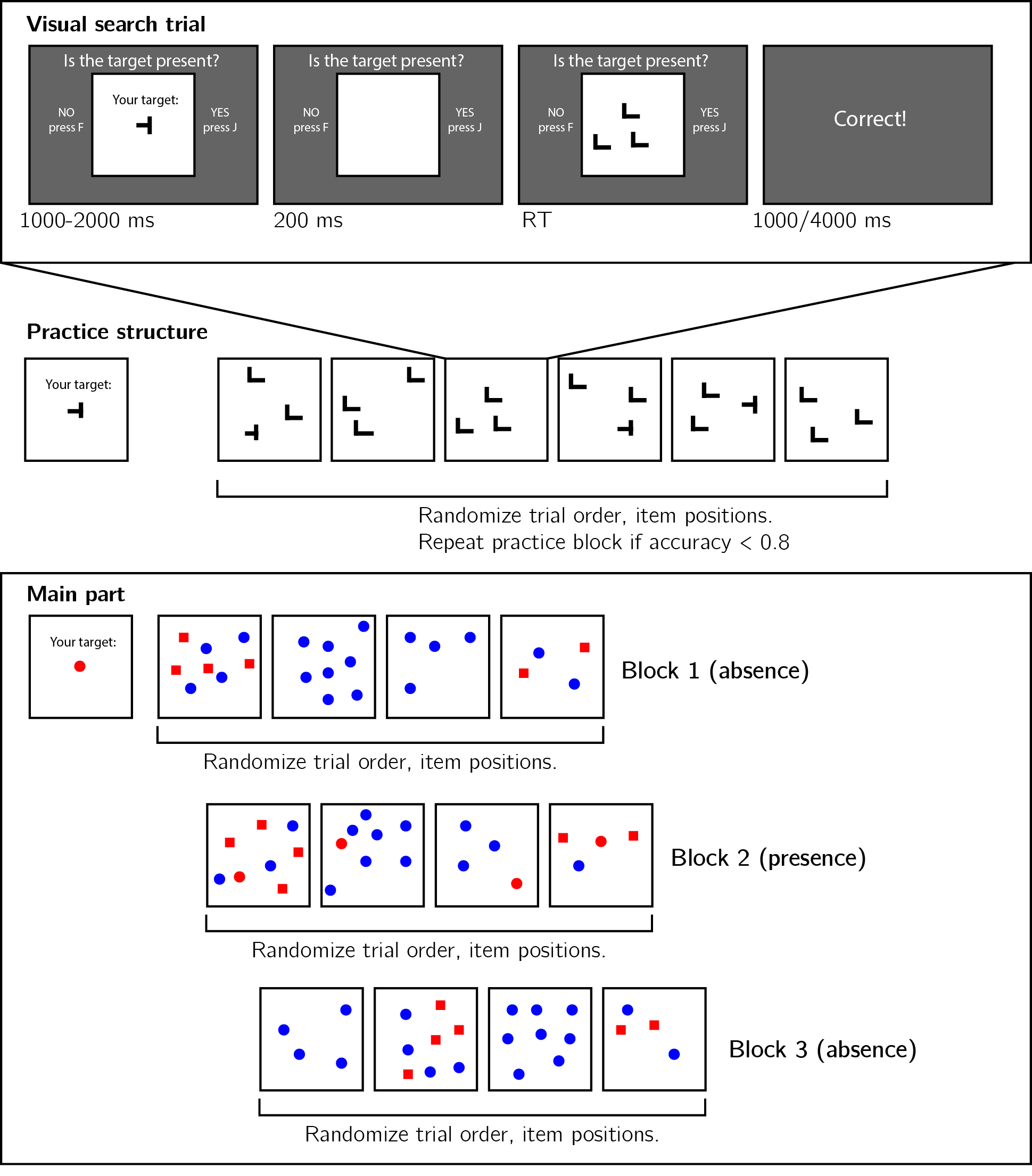
Figure 1.1: Experimental design. Top panel: each visual search trial started with a screen indicating the target stimulus. The search display remained visible until a response was recorded. To motivate accurate responses, the feedback screen remained visible for one second following correct responses and for four seconds following errors. Middle panel: after reading the instructions, participants practiced the visual search task in blocks of 6 trials, until they had reached an accuracy level of 0.83 correct or higher (at most one error in a block of 6 trials). Bottom panel: the main part of the experiment comprised 12 trials only, in which the target was a red dot. Unbeknown to subjects, only trials 5-8 (Block 2) were target-present trials, and the remaining trials were target-absent trials. Each 4-trial block followed a 2 by 2 design, with factors being set size (4 or 8) and distractor type (color or conjunction; blue dots only or blue dots and red squares, respectively).

In the main part of the experiment, participants searched for a red dot among blue dots or a mixed array of blue dots and red squares. Set size was set to 4 or 8, resulting in a 2-by-2 design (search type: color or color\(\times\)shape, by set size: 4 or 8). Critically, and unbeknown to subjects, the first four trials were always target-absent trials (one of each set-size \(\times\) search-type combination), presented in randomized order. These trials were followed by the four corresponding target-present trials, presented in randomized order. The final four trials were again target-absent trials, presented in randomized order.

1.2.3 Randomization

The order and timing of experimental events was determined pseudo-randomly by the Mersenne Twister pseudorandom number generator, initialized in a way that ensures registration time-locking (Mazor, Mazor, & Mukamel, 2019).

1.2.4 Data analysis

1.2.4.1 Rejection criteria

Participants were excluded for making more than one error in the main part of the experiment, or for having extremely fast or slow reaction times in one or more of the tasks (below 250 milliseconds or above 5 seconds in more than 25% of the trials).

Error trials, and trials with response times below 250 milliseconds or above 1 second were excluded from the response-time analysis. All pre-registered analyses without RT-based exclusion are reported in appendix B.

1.2.4.2 Data preprocessing

To control for within-block trial order effects, a linear regression model was fitted separately for each block and participant, predicting search time as a function of trial serial order within the block (\(RT \sim \beta_0+\beta_1i\), with \(i\) denoting the mean-centered serial position within a block). Search times were corrected by subtracting the product of the slope and the mean-centered serial position, in a block-wise manner.

Subject-wise search slopes were then extracted for each combination of search type (color or conjunction) and block number by fitting a linear regression model to the reaction time data with one intercept and one set-size term.

1.2.4.3 Hypotheses and analysis plan

Experiment 1 was designed to test several hypotheses about the contribution of metacognitive knowledge to search termination, the state of this knowledge prior to engaging with the task, and the effect of experience on this metacognitive knowledge. The specifics of our pre-registered analysis can be accessed in the following link: https://osf.io/ea385. We outline some possible search time patterns and their pre-registered interpretation in Fig. 1.2.

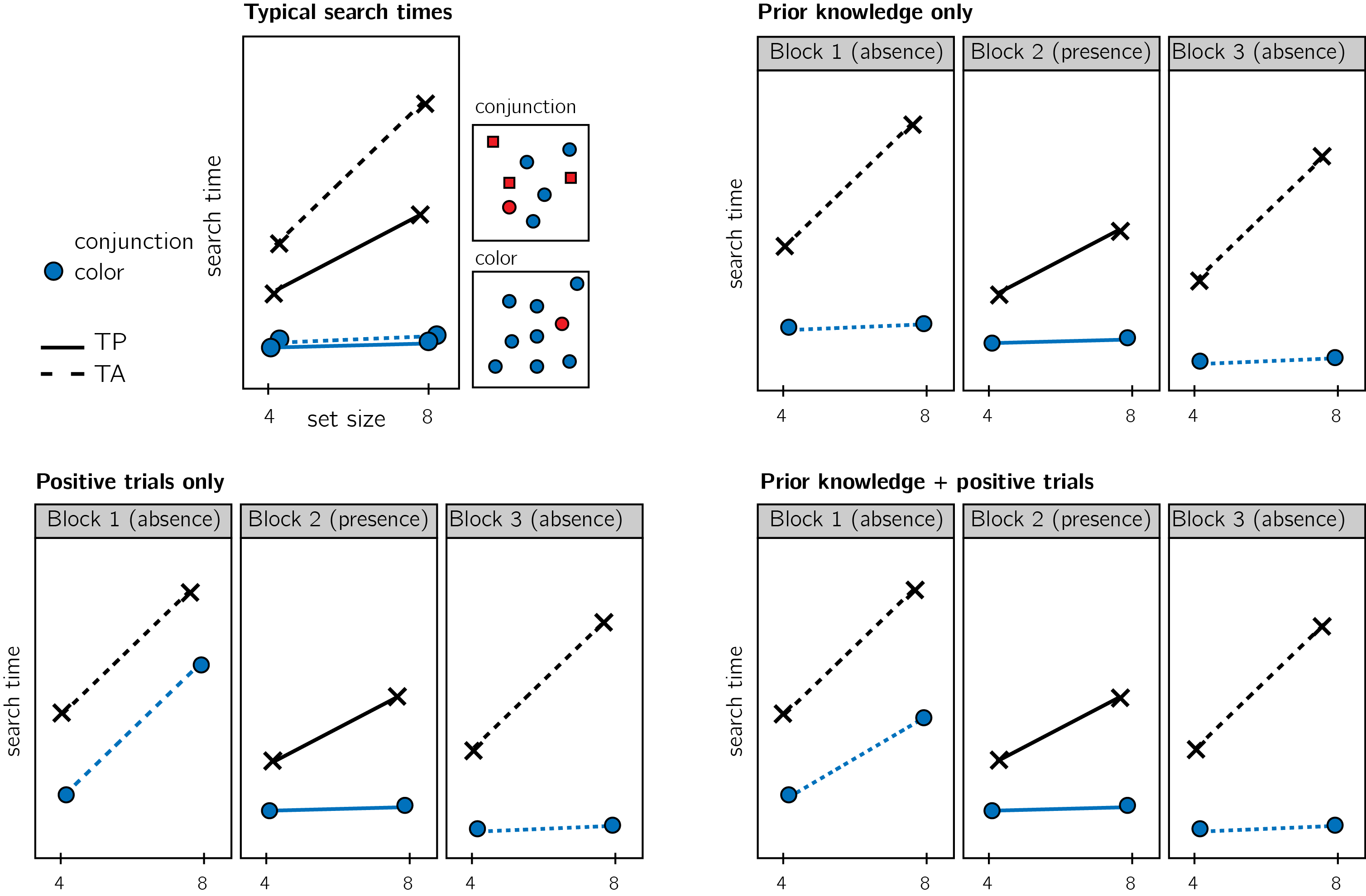
Figure 1.2: Visualization of Hypotheses. Top left: typical search times in visual search experiments with many trials (where TP = Target Present responses; TA = Target Absent responses). Set size (x axis) affects search time in conjunction search, but much less so in color search. However, it is unclear whether this pattern also holds in the first target-absent trials in an experiment. Different models make different predictions about target-absent search times in the first block of the experiment. Top right: one possibility is that the same qualitative pattern will be observed in our design, with an overall decrease in response time as a function of trial number. This would suggest that the second-order knowledge necessary to support efficient inference about absence was already in place before engaging with the task. Bottom left: an alternative pattern is that the same qualitative pattern will be observed for blocks 2 and 3, but not in block 1. This would suggest that for inference about absence to be efficient, participants had to first experience some target-present trials. Bottom right: alternatively, some degree of second-order knowledge may be available prior to engaging with the task, with some being acquired by subsequent exposure to target-present trials. This would manifest as different slopes for conjunction and color searches in blocks 1 and a learning effect for color search between blocks 1 and 3.

Analysis comprised a positive control based on target-present trials, a test of the presence of a pop-out effect for target-absent color search in block 1, and a test for the change in slope for target-absent color search between blocks 1 and 3. All hypotheses were tested using a within-subject t-test, with a significance level of 0.05. Given the fact that we only have one trial per cell, one excluded trial is sufficient to make some hypotheses impossible to test on a given participant. For this reason, for each hypothesis separately, participants were included only if all necessary trials met our inclusion criteria. This meant that some hypotheses were tested on different subsets of participants.

1.2.4.4 Transparency and Openness

We report how we determined our sample size, all data exclusions (if any), all manipulations, and all measures in the study. We used R [Version 4.0.5; R Core Team (2019)] and the R-packages BayesFactor [Version 0.9.12.4.2; Richard D. Morey & Rouder (2018)], cowplot [Version 1.1.1; Wilke (2019)], dplyr [Version 1.0.7; Wickham, François, Henry, & Müller (2020)], ggplot2 [Version 3.3.5; Wickham (2016)], jsonlite [Version 1.7.2; Ooms (2014)], lsr [Version 0.5; Navarro (2015)], MESS [Version 0.5.7; Ekstrøm (2019)], papaja [Version 0.1.0.9997; Aust & Barth (2020)], pwr [Version 1.3.0; Champely (2020)], reticulate [Version 1.20; Ushey, Allaire, & Tang (2020)], and tidyr [Version 1.1.3; Wickham & Henry (2020)] for all our analyses. A detailed pre-registration document for Experiment 1 can be accessed at osf.io/yh82v/. All analysis scripts and anonymized data are available at github.com/matanmazor/termination.

1.2.5 Results

Overall mean accuracy was 0.95 (standard deviation =0.06). Median reaction time was 623.98 ms (median absolute deviation = 127.37). In all further analyses, only correct trials with response times between 250 and 1000 ms are included.

Hypothesis 1 (positive control): Search times in block 2 (target-present) followed the expected pattern, with a steep slope for conjunction search (\(M = 12.52\), 95% CI \([10.08\), \(14.95]\)) and a shallow slope for color search (\(M = 3.91\), 95% CI \([2.13\), \(5.70]\); see middle panel in Fig. 1.3A). Color search slope was significantly lower than 10 ms/item and thus met our criterion for being considered ‘pop-out’ (\(t(961) = -6.69\), \(p < .001\)). Furthermore, the difference between the slopes was significant (\(t(749) = 6.50\), \(p < .001\)). This positive control served to validate our method of using two trials per participant for obtaining reliable group-level estimates of search slopes.

Hypothesis 2: Our central focus was on results from block 1 (target-absent). Here participants didn’t yet have experience with searching for the red dot. Similar to the second block, conjunction search slope was steep (\(M = 18.41\), 95% CI \([14.95\), \(21.87]\)). A clear pop-out effect for color absence was also evident (\(M = 0.15\), 95% CI \([-\infty\), \(2.31]\), \(t(886) = -7.51\), \(p < .001\)). Furthermore, the average search slope for color search in this first block was significantly different from that of the conjunction search (\(t(413) = 6.55\), \(p < .001\); see leftmost panel in Fig. 1.3A), indicating that a color-absence pop-out is already in place prior to direct task experience. This result is in line with the prior-knowledge only model (see Fig. 1.2), in which participants have valid expectations for efficient color search, prior to engaging with a task.

Pre-registered hypotheses 3-5 were designed to test for a learning effect between blocks 1 and 3, before and after experience with observing a red target among blue distractors. Given the overwhelming pop-out effect for target-absent trials in block 1, not much room for additional learning remained. Indeed, results from these tests support a prior-knowledge only model.

Hypothesis 3: Like in the first block, in the third block color search complied with our criterion for ‘pop-out’ (\(M = 2.27\), 95% CI \([-\infty\), \(3.86]\), \(t(979) = -7.98\), \(p < .001\)), and was significantly different from the conjunction search slope (\(t(745) = 11.16\), \(p < .001\); see rightmost panel in Fig. 1.3A). This result is not surprising, given that a pop-out effect was already observed in block 1.

Hypothesis 4: To quantify the learning effect for color search, we directly contrasted the search slope for color search in blocks 1 and 3. We find no evidence for a learning effect (\(t(799) = -1.15\), \(p = .250\)). Furthermore, a Bayesian t-test with a scaled Cauchy prior for effect sizes (r=0.707) provided strong evidence in favour of the absence of a learning effect (\(\mathrm{BF}_{\textrm{01}} = 12.98\)).

Hypothesis 5: In case of a learning effect for pop-out search, Hypothesis 5 was designed to test the specificity of this effect to color pop-out by computing an interaction between block number and search type. Given that no learning effect was observed, this test makes little sense. For completeness, we report that the change in slope between blocks 1 and 3 was similar for color and conjunction search (\(M = -3.58\), 95% CI \([-10.52\), \(3.36]\), \(t(320) = -1.01\), \(p = .311\)).

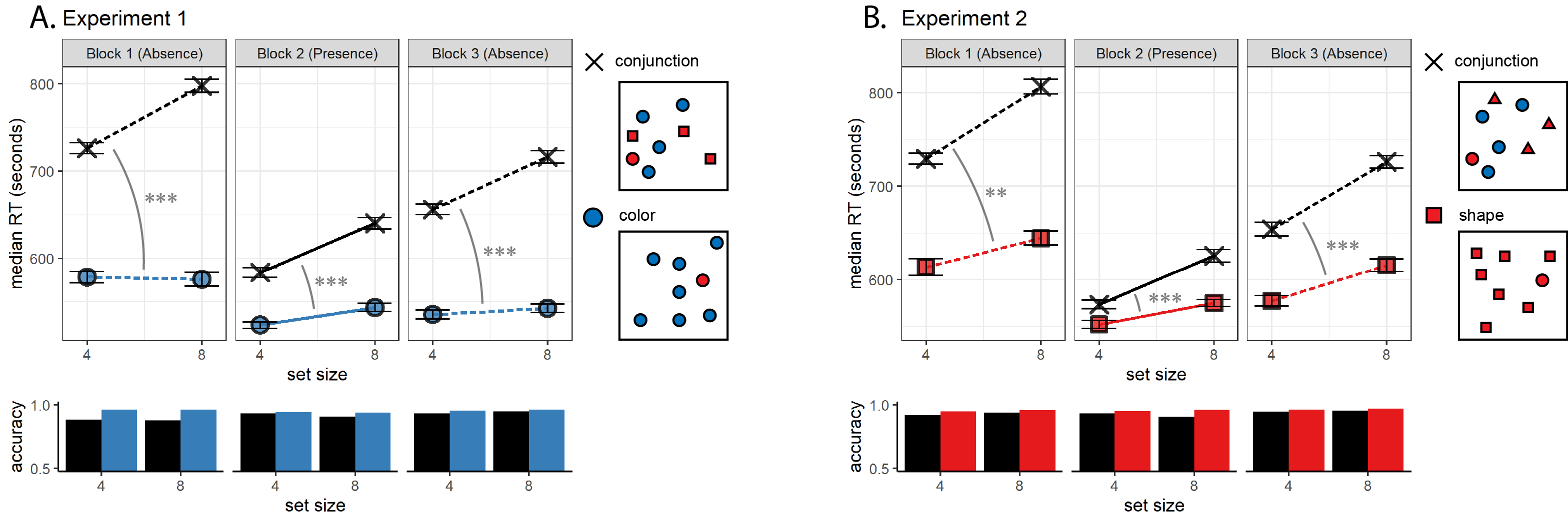
Figure 1.3: Main Results for Expeiments 1 (A) and 2 (B). Upper panel: median search time by distractor set size for the two search tasks across the three blocks (12 trials per participant). Correct responses only. Lower panel: accuracy as a function of block, set size and search type. Error bars represent the standard error of the median (estimated with bootstrapping). Significance stars correspond to the difference in slope between conjunction and feature search within a block. *: p<0.5, * * : p<0.01, * * * : p<0.001

1.2.6 Additional analysis: first trial only

We considered the possibility that our results do not reflect true absence pop-out without task experience, but instead might reflect participants’ ability to rapidly adjust their termination times based on feedback from previous trials, even within the four trials of the first block. To rule out such within-block learning effects, we tested whether participants showed a color-absence pop-out effect on the very first trial of the experiment. To this end, we analyzed first trial response times as a function of search type (conjunction or color) and set-size. Since these first trials were slower overall (median RT in the first trial: 881.30 ms compared to 630.34 ms in the last trial), for this exploratory analysis we did not exclude trials based on response times.

Even in this between-subject analysis, with only one trial per participant, we found a significant positive search slope for conjunction search (23.31 ms/item, \(p<0.01\)), but not for color search (-5.13 ms/item, \(p=.43\); note that this negative slope is not apparent in Fig. 1.4A because the figure presents median reaction times, rather than means). The difference in slopes between conjunction and color, quantified as the interaction between set size and search type in a two-way between-subject analysis of variance, was also significant (\(F(1, 1,041) = 6.74\), \(\mathit{MSE} = 466,761.60\), \(p = .010\), \(\hat{\eta}^2_G = .006\); see Fig. 1.4A). In other words, a color-absence pop-out was already detectable in the very first trial of the experiment.

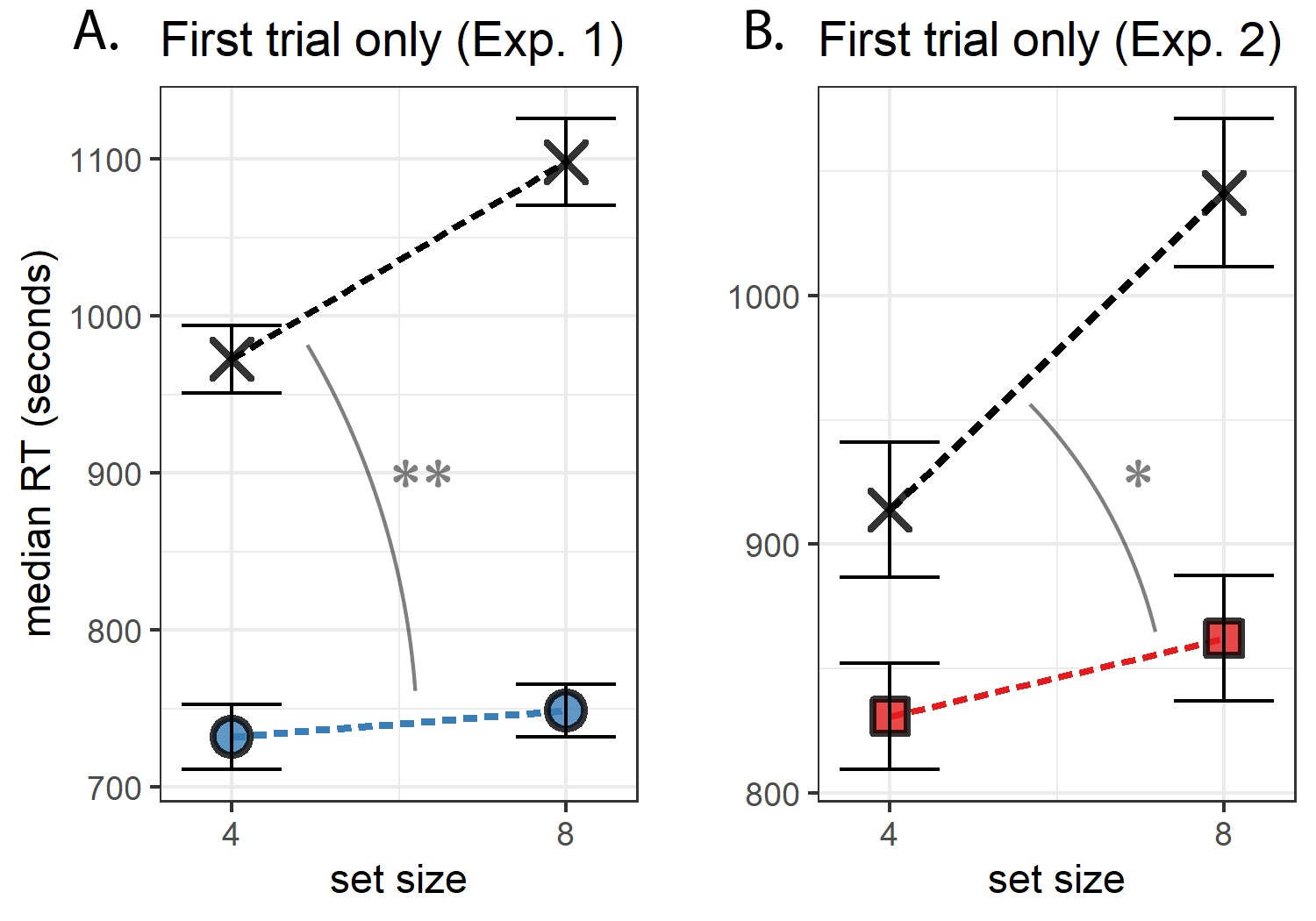
Figure 1.4: Median search time by distractor set size for Experiments 1 and 2, looking at the first trial of each participant only. Same conventions as in Fig. 1.3.

1.3 Experiment 2

Experiment 1 provided unequivocal evidence that color-absence pop-out occurs prior to experiencing color pop-out in the context of the same task. Experiment 2 was designed to extend these findings to another stimulus feature that is also found to efficiently guide attention: shape. Unlike colour space, which spans three dimensions only, the space of possible shapes is relatively unconstrained such that having prior knowledge of the expected effect of different shapes on attention might require a richer mental model of attentional processes. Furthermore, colour is agreed to be a ‘guiding attribute of attention,’ while it is unclear which shape features guide attention (J. M. Wolfe & Horowitz, 2017). In this experiment we also included an additional control for prior experience with visual search tasks, and asked if knowledge about search efficiency is available for explicit metacognitive report.

1.3.1 Participants

The research complied with all relevant ethical regulations, and was approved by the Research Ethics Committee of University College London (study ID number 1260/003). 887 participants (median reported age: 33; range: [18-75]) were recruited via Prolific, and gave their informed consent prior to their participation. They were selected based on their acceptance rate (>95%) and for being native English speakers. We collected data until we reached 320 included participants for hypotheses 1-4 (after applying our pre-registered exclusion criteria). The entire experiment took around 4 minutes to complete (median completion time in our pilot data: 3.93 minutes). Participants were paid £0.51 for their participation, equivalent to an hourly wage of £7.78.

1.3.2 Procedure

A static version of Experiment 2 can be accessed on matanmazor.github.io/termination. Experiment 2 was identical to Experiment 1 with the following exceptions. First, instead of color search trials, we included shape search trials, where the red dot target is present or absent in an array of red squares. Second, to minimize the similarity between conjunction and shape searches, conjunction trials included blue dots and red triangles as distractors. Third, to test participants’ explicit metacognition about their visual search behaviour, upon completing the main part of the task participants were presented with the four target-absent displays (shape and conjunction displays with 4 or 8 items), and were asked to sort them from fastest to slowest. Finally, participants reported whether they had participated in a similar experiment before, where they were asked to search for shapes on the screen. Participants who responded ‘yes’ were asked to tell us more about this previous experiment. This question was included in order to examine whether efficient target-absent search in trial 1 reflects prior experience with similar visual search experiments.

Our pre-registered analysis plan for Experiment 2, including rejection criteria and data preprocessing, was identical to our analysis plan for Experiment 1, and can be accessed in the following link: https://osf.io/v6mnb.

1.3.3 Results

Overall mean accuracy was 0.96 (standard deviation =0.06). Median reaction time was 644.60 ms (median absolute deviation = 123.89). In all further analyses, only correct trials with response times between 250 and 1000 ms are included.

Hypothesis 1 (positive control): Search times in block 2 (target-present) followed the expected pattern, with a steep slope for conjunction search (\(M = 15.08\), 95% CI \([12.34\), \(17.83]\)) and a shallow slope for shape search (\(M = 5.84\), 95% CI \([3.90\), \(7.78]\); see middle panel of Fig. 1.3B). The slope for shape search was significantly lower than 10 ms/item and thus met our criterion for being considered ‘pop-out’ (\(t(754) = -4.21\), \(p < .001\)). Furthermore, the difference between the slopes was significant (\(t(584) = 4.98\), \(p < .001\)).

Hypothesis 2: Our central focus was on results from block 1 (target-absent). Here participants didn’t yet have experience with finding the red dot. Similar to the second block, the slope for conjunction search was steep (\(M = 19.53\), 95% CI \([16.03\), \(23.04]\)). The slope for shape search was numerically lower than 10 ms/item, but not significantly so (\(M = 8.03\), 95% CI \([-\infty\), \(10.50]\), \(t(608) = -1.31\), \(p = .095\)). Still, the average search slope for shape search in this first block was significantly different from that of the conjunction search (\(t(326) = 2.77\), \(p = .006\); see leftmost panel of Fig. 1.3B), indicating that a processing advantage for detecting the absence of a shape compared to the absence of shape-color conjunction was already in place before experience with target presence.

Moreover, this processing advantage was not different from what is expected based on shape search slope in block 2 (target presence). A conservative estimate for the ratio between target absence and target presence search slopes is 2 (J. M. Wolfe, 1998). Based on this ratio of 2 and the observed target-presence search slope of 6 ms/item, target absence search slope is expected to be 12 ms/item, or higher. Indeed, search slope for shape absence was not significantly different from, and numerically lower than, twice the search slope for shape presence as measured in block 2 (\(t(548) = -1.16\), \(p = .246\); \(\mathrm{BF}_{\textrm{01}} = 10.66\)). In other words, our failure to find a pop-out effect for shape absence was not due to participants being suboptimal in their quitting times, but because finding a red dot among red squares is truly more difficult than finding a red dot among blue dots.

Hypothesis 3: As in the first block, in the third block the slope for shape search was numerically lower than 10 ms/item, but not significantly so (\(M = 8.85\), 95% CI \([-\infty\), \(10.68]\), \(t(723) = -1.03\), \(p = .151\)). Importantly, the slope for shape search in block 3 was significantly different from the slope for conjunction search (\(t(565) = 6.02\), \(p < .001\)) and not significantly different from twice the search slope for shape presence (\(t(653) = 1.04\), \(p = .299\); \(\mathrm{BF}_{\textrm{01}} = 13.29\); see rightmost panel of Fig. 1.3B).

Hypothesis 4: To quantify a potential learning effect for shape search between blocks 1 and 3, we directly contrasted the search slope for shape search in these two ‘target-absent’ blocks. We find no evidence for a learning effect (\(t(542) = -0.03\), \(p = .974\)). Furthermore, a Bayesian t-test with a scaled Cauchy prior for effect sizes (r=0.707) provided strong evidence against a learning effect (\(\mathrm{BF}_{\textrm{01}} = 20.72\)). Like in Experiment 1, these results are most consistent with a prior-knowledge only model (see Fig. 1.2), in which participants already know to expect that shape search should be easier than conjunction search, prior to having direct experience with target-present trials.

1.3.4 Additional Analyses

First trial only

As in Exp. 1, here we also extended our pre-registered analysis with an exploratory between-subject analysis, focusing on the first trial of the experiment. Here too, we observed a significant positive search slope for conjunction search (43.65 ms/item, \(p<0.001\)), but not for shape search (9.80 ms/item, \(p=.40\)). The difference in slopes between conjunction and shape, quantified as the interaction between set size and search type in a two-way betwee-subject analysis of variance, was significant (\(F(1, 781) = 4.25\), \(\mathit{MSE} = 209,989.78\), \(p = .040\), \(\hat{\eta}^2_G = .005\); see Fig. 1.4B). This result reveals that efficient recognition of shape absence is already detectable in the very first trial of the experiment.

Task experience

At the end of the experiment, participants were asked if they have ever participated in a similar experiment before, where they were asked to search for a target item. 796 out of 887 participants answered ‘no’ to this question. For those participants, a highly efficient search for a distinct shape in the first trials of the experiment, if found, cannot be due to prior experience of performing a visual search task with similar stimuli. Notably, however, participants who reported having no prior experience with a visual search task still showed efficient search termination for shape distractors (\(M = 7.32\), 95% CI \([4.21\), \(10.43]\)), and were significantly more efficient in terminating shape search than conjunction search in the first 4 target-absent trials (\(t(296) = 2.68\), \(p = .008\)). Efficient search termination for shape search is therefore not dependent on prior visual search trials, neither within the same experiment nor in previous ones.

Search time estimates

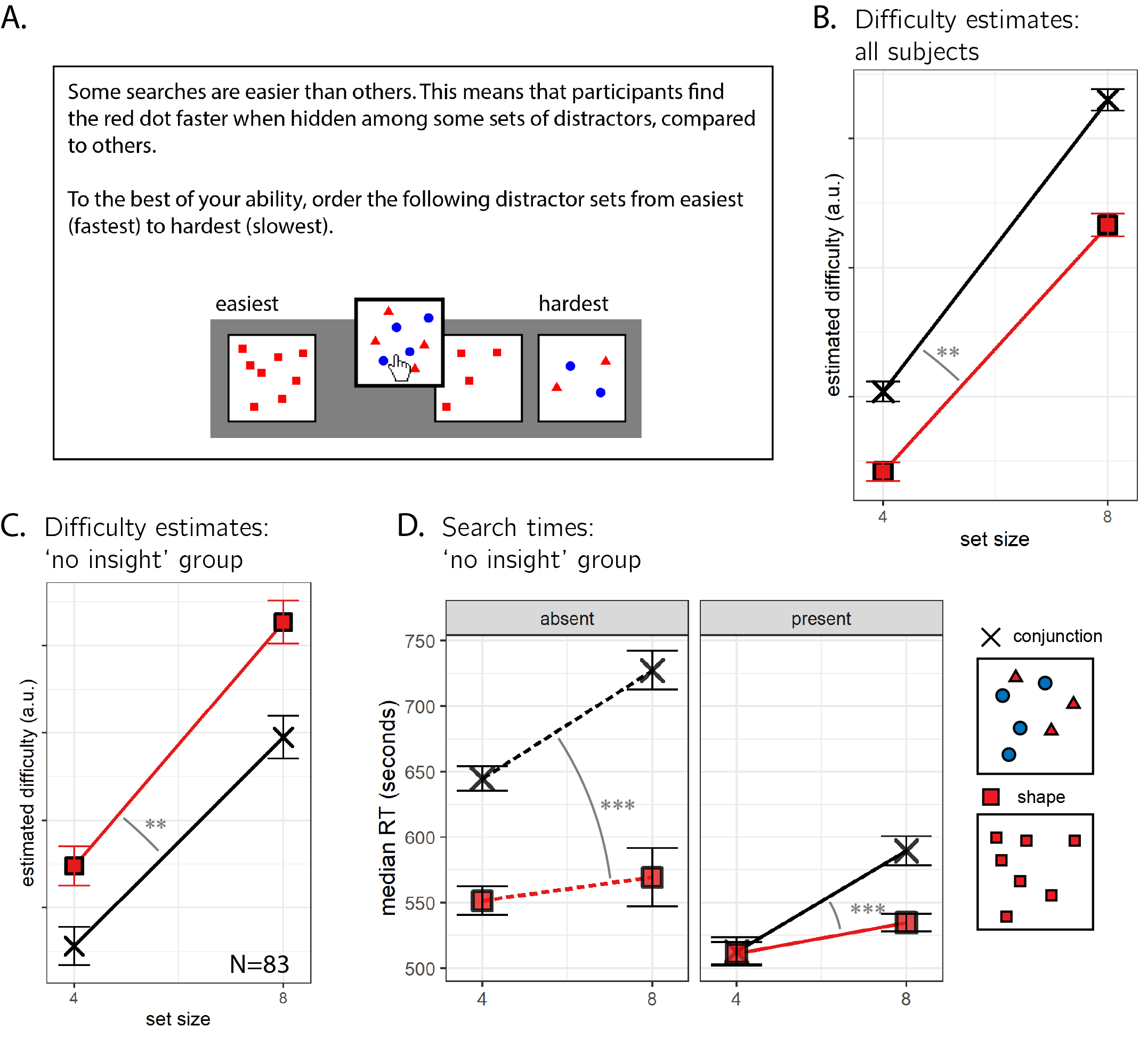
Figure 1.5: A: After completing the visual search component of Experiment 2, participants were asked to position the four searches (shape and conjunction searches with 4 or 8 distractors) on a perceived difficulty axis. B. As a group, participants’ estimates revealed metacognitive knowledge of the set size effect and of the fact that shape search is harder. C. A subset of 84 participants erroneously believed that shape search was more difficult than conjunction search. D. Even among these participants, search slopes in target-absence blocks followed the typical pattern, with a steeper slope for conjunction search. Same plotting conventions as Fig. 1.3.

Upon completing the main part of Experiment 2, participants positioned the four search arrays (shape and conjunction searches with 4 or 8 distractors) on a perceived difficulty axis (see Fig. 1.5A). We used these difficulty ratings to ask whether the advantage for detecting the absence of a distinct shape over the absence of a shape/color conjunction depended on explicit access to metacognitive knowledge about search difficulty. The decision to quit early in shape-absent trials may depend on an internal belief that the target shape would have drawn attention immediately, but this belief may be inaccessible to introspection. If introspective access is not a necessary condition for efficient quitting in visual search, some participants may not be able to reliably introspect about the difficulty of different searches but still be able to quit efficiently in shape search.

For this analysis, we only considered the ratings of participants who engaged with the array-sorting trial, and moved some of the arrays before continuing to the next trial (N=789). Searches with 8 distractors were rated as more difficult than searches with 4 distractors, in line with the set-size effect (\(t(788) = 31.62\), \(p < .001\)). Furthermore, conjunction searches were rated as more difficult than shape searches (\(t(788) = 5.11\), \(p < .001\)). Finally, we fitted single-subject linear regression models to the two search types, predicting search-time estimates (the position of each condition on a continuous perceived difficulty scale) as a function of set size. Similar to actual search slopes, these slopes derived from subjective estimates were also shallower for shape than for conjunction search, reflecting a belief that the effect of set size in shape search is not as strong as the effect of set size in conjunction search (\(M = 6.45\), 95% CI \([2.81\), \(10.08]\), \(t(788) = 3.48\), \(p = .001\); see Fig. 1.5B).

Subjective search time estimates revealed that by the end of the experiment, the average participant considered the slope of shape search to be shallower than that of conjunction search. This suggests that at least some participants had introspective access to their visual search behaviour. But were those participants whose estimates reflected a shallow slope for shape search the same ones that were more efficient in detecting the absence of a shape in the display? The slopes of retrospective estimates for shape search were not reliably correlated with actual search slopes for shape absence in block 1 (\(r = .08\), 95% CI \([-.06\), \(.22]\)) or 2 (\(r = .02\), 95% CI \([-.12\), \(.16]\)). However, this result should be interpreted carefully in light of the low reliability of single subject estimates that are derived from one trial per cell. Indeed, search slopes for shape absence in blocks 1 and 3 were not reliably correlated themselves (\(r = .05\), 95% CI \([-.10\), \(.19]\)).

To answer this question using a more severe test (Mayo, 2018), we focused on the subset of participants whose difficulty orderings reflected the erroneous belief that shape search was more difficult than conjunction search (\(N=\) 83; see Fig. 1.5C). If efficient search termination depends on accurate explicit metacognitive knowledge about search efficiency, search termination in this subset of participants is not expected to be more efficient in shape compared to conjunction search, and is even expected to show the opposite pattern. In contrast with this prediction, search slopes for shape-absence trials were shallower than for conjunction-absence trials (\(M_d = 12.45\), 95% CI \([5.21\), \(19.69]\), \(t(82) = 3.42\), \(p = .001\); see Fig. 1.5D). This indicates that efficient identification of shape absence is not dependent on explicit metacognitive knowledge about search efficiency.

1.4 Discussion

How do people decide that a target is absent from a visual scene? In this study we considered three candidate answers to this question: counterfactual reasoning (“I would have detected the target if it were present”), ensemble perception (“I immediately see that the target is missing”) and task heuristics (“Based on previous trials, responding now would balance accuracy and response time”). The third option is different from the first two: while a heuristic calibration of a termination rule may shape search behaviour in classic lab-based experiments comprised of many repetitive trials, it is not available to subjects in one-shot searches in their everyday lives, nor is it available to them in the first trial of the experiment.

To isolate the effect of previous trials on search termination, we focused on the first trials of a visual search task, before participants experience finding the target. Across two experiments, we found that no prior experience with color or shape pop-out in previous trials was needed for participants to be able to terminate the search early when a target would have been found immediately. In other words, participants were sensitive to the counterfactual efficiency with which a hypothetical target would have been detected even in the first trials of the experiment. This result rules out a purely heuristic-based account of search termination and suggests that in these first few trials, participants are relying on prior second-order knowledge about visual attention (e.g., ‘red pops out,’ or ‘a dot would catch my attention’), on a pre-attentional identification of target absence via ensemble statistics, or on a combination of the two.

Do participants employ a counterfactual heuristic, drawing on implicit metacognitive knowledge about search efficiency, or instead immediately perceive the absence of a target via ensemble scene statistics? We suggest that without second-order knowledge of their own perception and attention, ensemble perception alone is not sufficient to account for absence pop-out. Ensemble perception allows observers to extract summary statistical information from sets of similar stimuli, without directly perceiving any single stimulus (Whitney & Yamanashi Leib, 2018). According to this account, if participants immediately perceive that the search array comprises only squares, they might not need to rely on any counterfactual thinking or self-knowledge to conclude that no circle was present. Importantly, however, for the global statistical property ‘the array comprises only squares’ to be extracted from a display without representing individual squares, the visual system must represent, explicitly or implicitly, that a non-square item would have been detected by the visual system if they had been present. This second-order representation can be implemented, for example, as a threshold on curvature-sensitive neurons (‘a round object would have induced a higher firing rate in this neuron population’), or more generally as a likelihood function going from polygons to firing patterns (‘The perceived input is most likely under a world state where the display includes only polygons’).

As an illustration, assume that Sarah, a participant in our experiment, does not know that a red item would immediately catch her attention in an array of blue distractors. Not only can Sarah not report this fact, this knowledge is not represented and cannot influence her cognitive system. Sarah is now searching for a red dot, and sees a uniform array of blue dots. How can she know that she hasn’t missed a red dot? In the absence of second-order knowledge about search efficiency, Sarah would have to scan the dots one by one before committing to a ‘target absent’ response. Therefore, whether or not ensemble perception plays a role in absence pop-out, second-order knowledge about search efficiency is necessary to exlain the effects we observe.

Should this second-order knowledge be considered metacognitive? We argue that it should, and note that it is not a prerequisite for metacognitive knowledge to be accessible to consciousness. Metacognitive knowledge was originally assumed by Flavell (1979) to mostly affect cognition without accessing consciousness at all (i.e. without inducing a ‘metacognitive experience’). Different aspects of metacognitive monitoring, including an immediate Feeling of Knowing when presented with a problem, have been attributed to implicit metacognitive mechanisms that share a conceptual similarity with the ones described in the previous paragraph (Reder & Schunn, 1996). Indeed, metacognitive knowledge is sometimes measured as an ability to flexibly adapt information gathering thresholds: similar to a decision to terminate a search, the decision to stop gathering more information is widely accepted to be guided by metacognitive factors in developmental (Leckey et al., 2020; Siegel, Magid, Pelz, Tenenbaum, & Schulz, 2021) and comparative (Watanabe, Grodzinski, & Clayton, 2014) psychology.

Our findings complement and extend previous work in which participants had introspective awareness of attentional capture (Adams & Gaspelin, 2020, 2021): our results suggest that on top of the ability to monitor attention, people also hold valid second-order knowledge about attentional processes, that allows them to make predictions and guide their information gathering decisions. A schematic model of attention has been suggested to be implemented in the brains of many animal species, including all mammals and birds, and to facilitate attention control and monitoring (Graziano, 2013). This kind of implicit second-order knowledge, perhaps together with a capacity to extract ensemble statistics from a display, may be crucial for representing the absence of objects. The critical difference between inferring X is absent and simply lacking the belief X is present is a counterfactual belief that X would have been detected, had it been presented (Mazor, 2021; Mazor & Fleming, 2020). In turn, studying the processes underpinning efficient inference about absence can shed light on the role of higher-order representations in perception - because such counterfactual beliefs rest on representing, perhaps implicitly, how one’s own perceptual system might respond under various conditions.

1.5 Conclusion

Our findings reveal that some knowledge about search efficiency is available to participants already in the first trials of the experiment, before engaging with the task or knowing what distractors to expect. These results reflect the same qualitative response time patterns as those commonly obtained in typical (few subjects/many trials) visual search experiments. Given that no target was present in these trials, participants must have been sensitive to the counterfactual likelihood of them finding the target, had it been present. In Experiment 2 we showed that this second-order knowledge about search difficulty was often accessible to report, but that this was not a necessary condition for efficient search termination. We conclude that efficient inference about absence is critically dependent on implicit second-order knowledge about visual search. In the next chapter I look more closely at participants’ explicit second-order knowledge of their visual search behaviour, by asking for prospective search-time estimates for unfamiliar, complex stimuli.